- A solenoid is a long wire wound in a close-packed helix carrying a current I and the length of the solenoid is much greater than its diameter
- The figure below shows a section of a stretched out solenoid in xy and yz plane
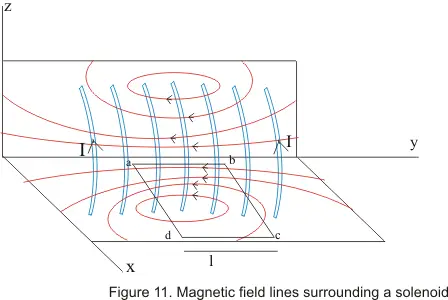
- The solenoid magnetic field is the vector sum of the field produced by the individual turns that make up the solenoid
- Magnetic field B is nearly uniform and parallel to the axis of the solenoid at interior points near its center and external field near the center is very small
- Consider a dashed closed path abcd as shown in figure .Let l be the length of side ab of the loop which is parallel to the is of the solenoid
- Let us also consider that sides bc and da of the loop are very-very long so that side cd is very much far away from the solenoid and magnetic field at this side is negligibly small and for simplicity we consider its equal to 0
- At side a magnetic field B is approximately parallel and constant. So for this side
∫B.dl=Bl - Magnetic field B is perpendicular to sides bc and da ,hence these portions of the loop does not make any contributions to the line integral as B.dl=0 for the side bc and da
- Side cd lies at external points solenoid where B.dl=0 as B=0 or negligibly small outside the solenoid
- Hence sum around the entire closed path reduces to Bl
- If N are number of turns per unit length in a solenoid then number of turns in length l is nl.The total current through the rectangle abcd is NIl and from ampere 's law
Bl=μ0NlI
or B=μ0NI (22) - we have obtained this relation for infinitely long solenoids considering the field at external points of the solenoid equal to zero.
- However for real solenoids external field is relatively weak rather then equal to zero
- Thus for actual solenoids relation 22 holds for internal points near the center of the solenoid
- Field at internal points of the solenoid does not depend on length and diameter of the solenoid and is uniform over the cross-section of a solenoid


 0
0

